ऑटोमेटा का सिद्धांत, परिमित ऑटोमेटा
विभिन्न मशीनों के संचालन की संरचना, डिजाइन, सिद्धांत काफी हद तक इसके कार्यात्मक उद्देश्य से निर्धारित होते हैं। तकनीकी, परिवहन, कंप्यूटिंग, सैन्य और अन्य मशीनों के बीच भेद। जटिल तकनीकी प्रक्रियाओं को करने के लिए डिज़ाइन किए गए संपूर्ण स्वचालित परिसरों को व्यापक रूप से विभिन्न उद्योगों में पेश किया जाता है। ऑटोमेटा को डिज़ाइन और निर्मित किया गया है जो विभिन्न तार्किक कार्यों (तार्किक मशीनों) का प्रदर्शन करता है।
ऑटोमेटा का सिद्धांत — साइबरनेटिक्स अनुभाग, जो डिजिटल कंप्यूटर और नियंत्रण मशीनों की प्रौद्योगिकी की आवश्यकताओं के प्रभाव में उत्पन्न हुआ। ऑटोमेटा सिद्धांत में अध्ययन किए गए असतत ऑटोमेटा वास्तविक प्रणालियों (तकनीकी और जैविक दोनों) के अमूर्त मॉडल हैं जो असतत समय चरणों में असतत (डिजिटल) जानकारी की प्रक्रिया करते हैं।
ऑटोमेटा सिद्धांत सटीक गणितीय अवधारणाओं पर आधारित है जो ऑटोमेटन के कामकाज (व्यवहार) और इसकी संरचना (आंतरिक संरचना) के बारे में सहज ज्ञान युक्त विचारों को औपचारिक रूप देता है।
इस मामले में, सूचना परिवर्तन को हमेशा एक ऑपरेशन के रूप में समझा जाता है जो इनपुट वर्णमाला से अक्षरों से बने इनपुट अनुक्रमों को आउटपुट वर्णमाला से अक्षरों से बने आउटपुट अनुक्रमों में परिवर्तित करता है।
गणितीय तर्क, बीजगणित, संभाव्यता सिद्धांत, संयोजक और ग्राफ सिद्धांत के तंत्र का व्यापक रूप से उपयोग किया जाता है।
इसके कुछ हिस्सों में ऑटोमेटा के सिद्धांत (ऑटोमेटा के संरचनात्मक सिद्धांत) के साथ समस्या बढ़ी रिले-संपर्क सर्किट के सिद्धांत से, जो 1930 के दशक के अंत में आकार लेने लगा। सहित तार्किक बीजगणित के तरीके.

ऑटोमेटा के संरचनात्मक सिद्धांत में, विभिन्न प्रकार की योजनाओं का अध्ययन किया जाता है, यह वर्णन करने के लिए डिज़ाइन किया गया है कि एक सिस्टम में ठीक से जुड़े सरल घटकों (तत्वों) से एक जटिल ऑटोमेटन कैसे बनाया जाता है।
एक अन्य दिशा, जिसे ऑटोमेटा का सार सिद्धांत कहा जाता है, ऑटोमेटा के व्यवहार का अध्ययन करती है (अर्थात, उनके द्वारा किए गए सूचना के परिवर्तन की प्रकृति), उनकी आंतरिक संरचना की बारीकियों से अलग करते हुए, और 1950 के दशक में उत्पन्न हुई।
ऑटोमेटा के सार सिद्धांत के ढांचे के भीतर, "ऑटोमेटन" और "मशीन" अवधारणाओं की सामग्री अनिवार्य रूप से एक ऑटोमेटन द्वारा की जाने वाली सूचना के परिवर्तन के मानक विवरण से समाप्त हो जाती है। ऐसा परिवर्तन नियतात्मक हो सकता है, लेकिन यह प्रकृति में संभाव्य भी हो सकता है।
सबसे अधिक अध्ययन नियतात्मक मशीनें (ऑटोमेटा) हैं, जिनमें परिमित ऑटोमेटा शामिल है - ऑटोमेटा के सिद्धांत में अध्ययन का मुख्य उद्देश्य।
एक परिमित राज्य मशीन को सीमित मात्रा में मेमोरी (आंतरिक राज्यों की संख्या) की विशेषता है और इसे एक संक्रमण फ़ंक्शन का उपयोग करके परिभाषित किया गया है।कुछ उचित आदर्शीकरण के साथ, सभी आधुनिक गणितीय मशीनों और यहाँ तक कि मस्तिष्क को, उनके कामकाज के दृष्टिकोण से, परिमित ऑटोमेटा के रूप में माना जा सकता है।
"अनुक्रमिक मशीन", "मिली ऑटोमेटन", "मूर ऑटोमेटन" शब्द साहित्य में उपयोग किए जाते हैं (और सभी लेखकों द्वारा समान रूप से नहीं) "परिमित ऑटोमेटन" शब्द के समानार्थक शब्द के रूप में या एक परिमित के संक्रमण कार्यों में कुछ विशेषताओं पर जोर देने के लिए automaton.
असीमित मेमोरी के साथ ऑटोमेटा एक ट्यूरिंग मशीन है जो किसी भी कुशल सूचना परिवर्तन (संभावित रूप से) को करने में सक्षम है। "ट्यूरिंग मशीन" की अवधारणा "परिमित राज्य मशीन" की अवधारणा से पहले उठी और मुख्य रूप से एल्गोरिदम के सिद्धांत में अध्ययन किया जाता है।
सार ऑटोमेटा सिद्धांत प्रसिद्ध बीजगणितीय सिद्धांतों से निकटता से संबंधित है, उदाहरण के लिए सेमीग्रुप सिद्धांत। लागू दृष्टिकोण से, स्मृति आकार के संदर्भ में एक ऑटोमेटन में सूचना के परिवर्तन की विशेषता वाले परिणाम रुचि के हैं।
यह मामला है, उदाहरण के लिए, ऑटोमेटा (ई.एफ. मूर, आदि द्वारा काम करता है) पर प्रयोगों के साथ समस्याओं में, जहां ऑटोमेटन के संक्रमण कार्यों के बारे में एक या दूसरी जानकारी या इसकी मेमोरी की क्षमता के परिणामों से प्राप्त की जाती है प्रयोग।
एक अन्य कार्य ऑटोमेटन की मेमोरी के आकार और इनपुट अनुक्रमों की अवधि के बारे में उपलब्ध जानकारी के आधार पर आउटपुट अनुक्रमों की अवधि की गणना करना है।
परिमित राज्य मशीनों की स्मृति को कम करने और यादृच्छिक वातावरण में उनके व्यवहार का अध्ययन करने के तरीकों का विकास बहुत महत्वपूर्ण है।
अमूर्त ऑटोमेटा सिद्धांत में, संश्लेषण समस्या निम्नलिखित है।कुछ स्पष्ट रूप से औपचारिक भाषा के संदर्भ में, डिज़ाइन किए गए ऑटोमेटन के व्यवहार के लिए शर्तें लिखी गई हैं (ऑटोमेटन में दर्शाई गई घटना के लिए)। इस मामले में, विधियों को विकसित करना आवश्यक है जो प्रत्येक लिखित स्थिति के अनुसार:
1) पता करें कि क्या ऐसी राज्य मशीन मौजूद है कि इसके द्वारा परिवर्तित की गई जानकारी इस स्थिति को पूरा करती है;
2) यदि हाँ, तो ऐसी परिमित अवस्था मशीन के संक्रमण कार्यों का निर्माण किया जाता है या इसकी मेमोरी के आकार का अनुमान लगाया जाता है।
इस तरह के सूत्रीकरण में संश्लेषण कार्य का समाधान रिकॉर्डिंग से सकर्मक कार्यों में संक्रमण के लिए सुविधाजनक एल्गोरिदम के साथ एक ऑटोमेटन की परिचालन स्थितियों को रिकॉर्ड करने के लिए एक सुविधाजनक भाषा के प्रारंभिक निर्माण को निर्धारित करता है।
ऑटोमेटा के संरचनात्मक सिद्धांत में, संश्लेषण की समस्या में किसी दिए गए प्रकार के तत्वों की एक श्रृंखला का निर्माण होता है जो कि इसके संक्रमण कार्यों द्वारा दिए गए एक परिमित automaton को महसूस करता है। इस मामले में, वे आमतौर पर कुछ इष्टतमता मानदंड बताते हैं (उदाहरण के लिए, तत्वों की न्यूनतम संख्या) और एक इष्टतम योजना प्राप्त करना चाहते हैं।
जैसा कि बाद में पता चला, इसका मतलब है कि रिले-संपर्क सर्किट के संबंध में पहले विकसित कुछ तरीके और अवधारणाएं दूसरे प्रकार के सर्किट पर लागू होती हैं।
इलेक्ट्रॉनिक प्रौद्योगिकियों के विकास के संबंध में, सबसे व्यापक योजनाएं हैं कार्यात्मक तत्वों की (तार्किक नेटवर्क)। तर्क नेटवर्क का एक विशेष मामला सार तंत्रिका नेटवर्क है, जिसके तत्वों को न्यूरॉन्स कहा जाता है।
संश्लेषण के कई तरीके विकसित किए गए हैं, सर्किट के प्रकार और सूचना के परिवर्तन के आधार पर जिसके लिए उनका इरादा है (रिले उपकरणों का संश्लेषण)।
देखना -संयोजन परिपथों का न्यूनीकरण, कार्नाट मानचित्र, परिपथ संश्लेषण
परिमित अवस्था मशीन - निश्चित (संचालन के दौरान बढ़ने में असमर्थ) स्मृति आकार के साथ एक नियंत्रण प्रणाली का एक गणितीय मॉडल।
एक परिमित राज्य मशीन की अवधारणा एक गणितीय अमूर्तता है जो नियंत्रण प्रणालियों के एक सेट की सामान्य विशेषताओं की विशेषता है (उदाहरण के लिए, एक मल्टी-लूप रिले डिवाइस)। ऐसी सभी प्रणालियों में सामान्य विशेषताएं होती हैं जिन्हें परिमित ऑटोमेटन की परिभाषा के रूप में स्वीकार करना स्वाभाविक है।
प्रत्येक पूर्ण ऑटोमेटन में बाहरी प्रभावों और आंतरिक तत्वों के लिए एक प्रवेश द्वार होता है। इनपुट और आंतरिक तत्वों दोनों के लिए, असतत राज्यों की एक निश्चित संख्या होती है जो वे ले सकते हैं।
इनपुट और आंतरिक तत्वों की अवस्थाओं में परिवर्तन समय के असतत क्षणों में होता है, जिसके बीच के अंतराल को टिक कहा जाता है। टेप के अंत में आंतरिक स्थिति (आंतरिक स्थिति) पूरी तरह से आंतरिक स्थिति और टेप की शुरुआत में इनपुट की स्थिति द्वारा निर्धारित की जाती है।
परिमित automaton की अन्य सभी परिभाषाओं को इस विशेषता में कम किया जा सकता है, विशेष परिभाषाओं में जो मानते हैं कि एक परिमित automaton का आउटपुट होता है जो किसी निश्चित समय पर automaton की आंतरिक स्थिति पर निर्भर करता है।
इस तरह की विशेषता के संदर्भ में, इसके इनपुट और आंतरिक राज्यों की प्रकृति पूर्ण ऑटोमेटन के विवरण के लिए अप्रासंगिक है। इनपुट्स और स्टेट्स के बजाय, आप उनकी संख्या को रैंडम नंबरिंग में देख सकते हैं।
यदि पिछले आंतरिक राज्य संख्या और पिछले इनपुट राज्य संख्या पर इसकी आंतरिक स्थिति संख्या की निर्भरता निर्दिष्ट की जाती है, तो राज्य मशीन सेट की जाएगी। ऐसा कार्य अंतिम तालिका के रूप में हो सकता है।
एक पूर्ण ऑटोमेटन को परिभाषित करने का एक अन्य सामान्य तरीका तथाकथित का निर्माण है संक्रमण आरेख। इनपुट राज्यों को अक्सर केवल इनपुट कहा जाता है, और आंतरिक राज्य केवल राज्य होते हैं।
एक परिमित राज्य मशीन तकनीकी उपकरणों और कुछ जैविक प्रणालियों दोनों का एक मॉडल हो सकती है। पहले प्रकार के ऑटोमेटा हैं, उदाहरण के लिए, रिले डिवाइस और विभिन्न इलेक्ट्रॉनिक कंप्यूटर, सहित। प्रोग्राम करने योग्य तर्क नियंत्रक.
रिले डिवाइस के मामले में, इनपुट स्टेट्स की भूमिका रिले डिवाइस के संवेदनशील तत्वों के राज्यों के संयोजन द्वारा निभाई जाती है (ऐसे राज्यों का प्रत्येक संयोजन एक "जटिल स्थिति" है, जो सभी संवेदनशील तत्वों के संकेत द्वारा विशेषता है ये असतत कहते हैं कि उनके पास एक निश्चित क्षण में है)। इसी तरह, रिले डिवाइस के मध्यवर्ती तत्वों के राज्यों के संयोजन आंतरिक राज्यों के रूप में कार्य करते हैं।
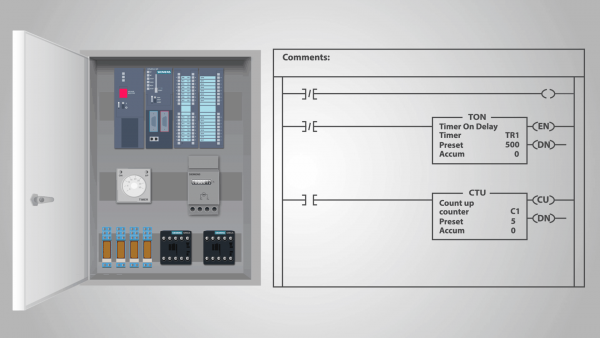
प्रोग्रामेबल लॉजिक कंट्रोलर (पीएलसी) एक रिले एक्शन डिवाइस का एक उदाहरण है जिसे स्टैंड-अलोन स्टेट मशीन कहा जा सकता है।
वास्तव में, एक बार जब कार्यक्रम पीएलसी में प्रवेश कर जाता है और नियंत्रक गणना करना शुरू कर देता है, तो यह बाहरी प्रभावों के संपर्क में नहीं आता है और प्रत्येक बाद की स्थिति पूरी तरह से अपनी पिछली स्थिति से निर्धारित होती है। हम मान सकते हैं कि प्रत्येक घड़ी चक्र में इनपुट की स्थिति समान है।
इसके विपरीत, कोई भी परिमित राज्य मशीन जिसमें केवल संभव इनपुट स्थिति होती है, स्वाभाविक रूप से स्वायत्त कहलाती है, क्योंकि इस मामले में बाहरी वातावरण में कोई जानकारी नहीं होती है जो उसके व्यवहार को नियंत्रित करती है।
यह सभी देखें:
पीएलसी के उपयोग के उदाहरण पर इलेक्ट्रिकल इंजीनियरिंग में माइक्रोप्रोसेसर सिस्टम का उपयोग