एक विद्युत क्षेत्र में एक इलेक्ट्रॉन

एक विद्युत क्षेत्र में एक इलेक्ट्रॉन का संचलन इलेक्ट्रिकल इंजीनियरिंग के लिए सबसे महत्वपूर्ण भौतिक प्रक्रियाओं में से एक है। चित्र देखते हैं कि निर्वात में यह कैसे होता है। आइए पहले एक समान विद्युत क्षेत्र में कैथोड से एनोड तक एक इलेक्ट्रॉन की गति का एक उदाहरण लें।

नीचे दिया गया आंकड़ा एक स्थिति दिखाता है जहां इलेक्ट्रॉन नकारात्मक इलेक्ट्रोड (कैथोड) को नगण्य रूप से छोटे प्रारंभिक वेग (शून्य की ओर प्रवृत्त) के साथ छोड़ देता है और प्रवेश करता है एक समान विद्युत क्षेत्र मेंदो इलेक्ट्रोड के बीच मौजूद।

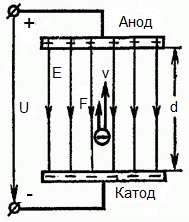
एक स्थिर वोल्टेज यू इलेक्ट्रोड पर लागू होता है, और विद्युत क्षेत्र में एक समान ताकत ई होती है। इलेक्ट्रोड के बीच की दूरी डी के बराबर होती है। इस स्थिति में, एक बल F क्षेत्र के किनारे से इलेक्ट्रॉन पर कार्य करेगा, जो इलेक्ट्रॉन के आवेश और क्षेत्र की शक्ति के समानुपाती होता है:

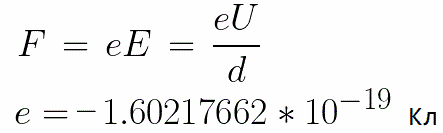
चूँकि इलेक्ट्रॉन पर ऋणात्मक आवेश होता है, यह बल क्षेत्र शक्ति सदिश E के विरुद्ध निर्देशित होगा। तदनुसार, विद्युत क्षेत्र द्वारा इलेक्ट्रॉन को उस दिशा में त्वरित किया जाएगा।

इलेक्ट्रॉन द्वारा अनुभव किया गया त्वरण उस पर कार्य करने वाले बल F के परिमाण के समानुपाती होता है और इलेक्ट्रॉन के द्रव्यमान m के व्युत्क्रमानुपाती होता है।चूँकि क्षेत्र एक समान है, किसी दिए गए चित्र के लिए त्वरण को इस प्रकार व्यक्त किया जा सकता है:

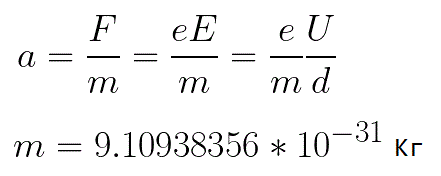
इस सूत्र में, इलेक्ट्रॉन के आवेश का उसके द्रव्यमान से अनुपात इलेक्ट्रॉन का विशिष्ट आवेश है, एक मात्रा जो एक भौतिक स्थिरांक है:

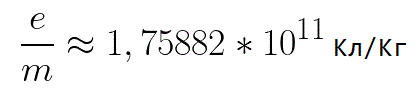
तो इलेक्ट्रॉन एक त्वरित विद्युत क्षेत्र में है क्योंकि प्रारंभिक वेग की दिशा v0 क्षेत्र के बल F की दिशा के साथ मेल खाता है और इसलिए इलेक्ट्रॉन समान रूप से चलता है। यदि कोई बाधा नहीं है, तो यह इलेक्ट्रोड के बीच पथ d की यात्रा करेगा और एक निश्चित गति v के साथ एनोड (पॉजिटिव इलेक्ट्रोड) तक पहुंचेगा। उस समय जब इलेक्ट्रॉन एनोड पर पहुंचता है, इसकी गतिज ऊर्जा इसके बराबर होगी:

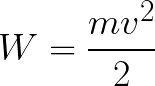
चूँकि पूरे पथ d के साथ इलेक्ट्रॉन विद्युत क्षेत्र की शक्तियों द्वारा त्वरित होता है, इसलिए यह गतिज ऊर्जा क्षेत्र के पक्ष में कार्य करने वाले बल द्वारा किए गए कार्य के परिणामस्वरूप प्राप्त करता है। यह कार्य इसके बराबर है:

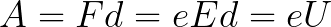
फिर क्षेत्र में गतिमान इलेक्ट्रॉन द्वारा अर्जित गतिज ऊर्जा को निम्न प्रकार से पाया जा सकता है:

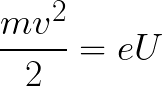
अर्थात्, यह संभावित अंतर U वाले बिंदुओं के बीच एक इलेक्ट्रॉन को गति देने के लिए क्षेत्र बलों के कार्य से अधिक कुछ नहीं है।

ऐसी स्थितियों में, एक इलेक्ट्रॉन की ऊर्जा को व्यक्त करने के लिए, माप की ऐसी इकाई को "इलेक्ट्रॉन वोल्ट" के रूप में उपयोग करना सुविधाजनक होता है, जो 1 वोल्ट के वोल्टेज पर एक इलेक्ट्रॉन की ऊर्जा के बराबर होता है। और चूँकि इलेक्ट्रॉन आवेश स्थिर है, तो 1 इलेक्ट्रोवोल्ट भी एक स्थिर मान है:

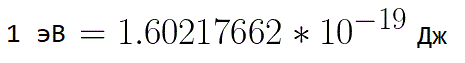
पिछले सूत्र से, आप एक त्वरित विद्युत क्षेत्र में चलते समय अपने पथ पर किसी भी बिंदु पर इलेक्ट्रॉन की गति को आसानी से निर्धारित कर सकते हैं, केवल उस संभावित अंतर को जानते हुए जिसे वह गति करते समय पारित करता है:

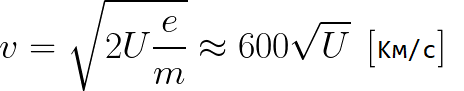
जैसा कि हम देख सकते हैं, एक त्वरित क्षेत्र में एक इलेक्ट्रॉन की गति केवल अंतिम बिंदु और उसके पथ के प्रारंभ बिंदु के बीच संभावित अंतर U पर निर्भर करती है।

कल्पना कीजिए कि इलेक्ट्रॉन नगण्य गति से कैथोड से दूर जाने लगता है, और कैथोड और एनोड के बीच वोल्टेज 400 वोल्ट है। इस स्थिति में, एनोड पर पहुँचने के क्षण में, इसकी गति इसके बराबर होगी:

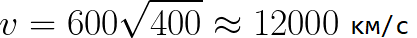
इलेक्ट्रोड के बीच दूरी d की यात्रा करने के लिए इलेक्ट्रॉन के लिए आवश्यक समय निर्धारित करना भी आसान है। विरामावस्था से एकसमान त्वरित गति से औसत गति अंतिम गति की आधी पाई जाती है, तो विद्युत क्षेत्र में त्वरित उड़ान का समय बराबर होगा:

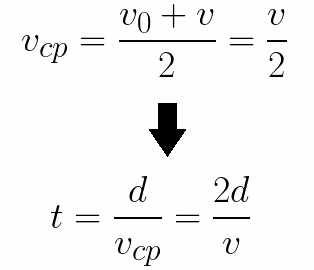
आइए अब एक उदाहरण पर विचार करें जब एक इलेक्ट्रॉन एक समान गति वाले विद्युत क्षेत्र में चलता है। अर्थात, क्षेत्र पहले की तरह निर्देशित होता है, लेकिन इलेक्ट्रॉन विपरीत दिशा में चलना शुरू कर देता है - एनोड से कैथोड तक।

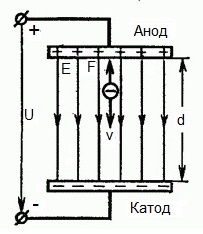
मान लीजिए कि इलेक्ट्रॉन ने एनोड को कुछ प्रारंभिक वेग v के साथ छोड़ दिया और शुरू में कैथोड की दिशा में आगे बढ़ना शुरू कर दिया। इस मामले में, विद्युत क्षेत्र की ओर से इलेक्ट्रॉन पर कार्य करने वाले बल F को विद्युत तीव्रता वेक्टर E - कैथोड से एनोड तक निर्देशित किया जाएगा।

यह इलेक्ट्रॉन की प्रारंभिक गति को कम करना शुरू कर देगा, अर्थात क्षेत्र इलेक्ट्रॉन को धीमा कर देगा। इसका अर्थ है कि इन परिस्थितियों में इलेक्ट्रॉन समान रूप से और समान रूप से धीरे-धीरे चलना शुरू कर देगा। स्थिति को इस प्रकार वर्णित किया गया है: "एक इलेक्ट्रॉन एक घटते हुए विद्युत क्षेत्र में गति करता है।"

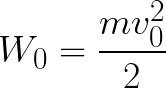
एनोड से, इलेक्ट्रॉन गैर-शून्य गतिज ऊर्जा के साथ चलना शुरू कर दिया, जो मंदी के दौरान घटने लगता है, क्योंकि ऊर्जा अब इलेक्ट्रॉन पर क्षेत्र से कार्य करने वाले बल पर काबू पाने में खर्च होती है।

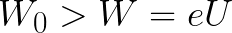
यदि एनोड से बाहर निकलने पर इलेक्ट्रॉन की प्रारंभिक गतिज ऊर्जा उस ऊर्जा से तुरंत अधिक होती है जिसे कैथोड से एनोड तक जाने में इलेक्ट्रॉन को गति देने के लिए क्षेत्र द्वारा खर्च किया जाना चाहिए (जैसा कि पहले उदाहरण में), तो इलेक्ट्रॉन होगा d दूरी तय करता है और अंतत: ब्रेकिंग के बावजूद कैथोड तक पहुंच जाएगा।

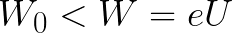
यदि इलेक्ट्रॉन की प्रारंभिक गतिज ऊर्जा इस महत्वपूर्ण मान से कम है, तो इलेक्ट्रॉन कैथोड तक नहीं पहुंचेगा। एक निश्चित बिंदु पर यह बंद हो जाएगा, फिर एनोड पर वापस समान रूप से त्वरित गति शुरू करें। नतीजतन, क्षेत्र उस ऊर्जा को वापस कर देगा जो रोकने की प्रक्रिया में खर्च की गई थी।

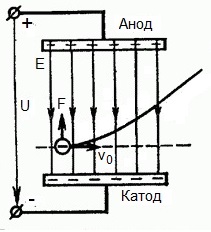
लेकिन क्या होगा अगर एक इलेक्ट्रॉन समकोण पर विद्युत क्षेत्र की क्रिया के क्षेत्र में v0 गति से उड़ता है? जाहिर है, इस क्षेत्र में क्षेत्र की ओर बल को कैथोड से एनोड तक इलेक्ट्रॉन के लिए निर्देशित किया जाता है, अर्थात विद्युत क्षेत्र की ताकत वेक्टर ई के खिलाफ।

इसका मतलब यह है कि अब इलेक्ट्रॉन में गति के दो घटक होते हैं: पहला - क्षेत्र के लंबवत v0 वेग के साथ, दूसरा - एनोड की ओर निर्देशित क्षेत्र की ओर से बल की कार्रवाई के तहत समान रूप से त्वरित होता है।

यह पता चला है कि, क्रिया के क्षेत्र में प्रवाहित होने के बाद, इलेक्ट्रॉन एक परवलयिक प्रक्षेपवक्र के साथ चलता है। लेकिन क्षेत्र की कार्रवाई के क्षेत्र से बाहर उड़ने के बाद, इलेक्ट्रॉन एक सीधी रेखा प्रक्षेपवक्र के साथ जड़ता से अपनी समान गति जारी रखेगा।