निरंतर दोलन और पैरामीट्रिक अनुनाद

निरंतर कंपन - ऐसे कंपन जिनकी ऊर्जा समय के साथ नहीं बदलती। वास्तविक भौतिक प्रणालियों में, हमेशा ऐसे कारण होते हैं जो कंपन ऊर्जा को तापीय ऊर्जा में बदलने का कारण बनते हैं (जैसे यांत्रिक प्रणालियों में घर्षण, विद्युत प्रणालियों में सक्रिय प्रतिरोध)।

इसलिए, अवमंदित दोलनों को केवल तभी प्राप्त किया जा सकता है जब इन ऊर्जा हानियों की पूर्ति की जाए। बाहरी स्रोत से ऊर्जा के कारण स्व-दोलन प्रणालियों में ऐसी पुनःपूर्ति स्वचालित रूप से होती है। निरंतर विद्युत चुम्बकीय दोलनों का व्यापक रूप से उपयोग किया जाता है। उन्हें प्राप्त करने के लिए विभिन्न जनरेटर का उपयोग किया जाता है।

विद्युत या यांत्रिक कंपन (एक दोलन चक्र या पेंडुलम के) को अवमंदित करने के लिए, हर समय प्रतिरोध या घर्षण नुकसान की भरपाई करना आवश्यक है।

उदाहरण के लिए, आप एक वैकल्पिक ईएमएफ के साथ दोलन सर्किट पर कार्य कर सकते हैं, जो समय-समय पर कॉइल में करंट बढ़ाएगा और तदनुसार, कैपेसिटर में वोल्टेज आयाम बनाए रखेगा।या आप पेंडुलम को इसी तरह से धक्का दे सकते हैं, इसे सामंजस्यपूर्ण रूप से झूलते हुए।

जैसा कि आप जानते हैं, दोलन परिपथ की कुंडली के चुंबकीय क्षेत्र की ऊर्जा का परिमाण इसके प्रेरकत्व और धारा से निम्नलिखित संबंध द्वारा संबंधित है (दूसरा सूत्र हैसंधारित्र के विद्युत क्षेत्र की ऊर्जा समान समोच्च समोच्च)

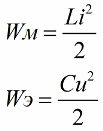
पहले सूत्र से यह स्पष्ट है कि यदि हम समय-समय पर वैकल्पिक EMF सर्किट पर कार्य करते हुए कॉइल में करंट बढ़ाते हैं, तो (फॉर्मूला - करंट में दूसरे कारक को बढ़ाकर या घटाकर) हम समय-समय पर इस सर्किट को ऊर्जा से भर देंगे।

अपने प्राकृतिक मुक्त दोलनों के साथ समय पर सर्किट पर सख्ती से कार्य करना, यानी गुंजयमान आवृत्ति पर, हमें विद्युत अनुनाद की घटना मिलेगी, क्योंकि यह गुंजयमान आवृत्ति पर है दोलन प्रणाली सबसे अधिक तीव्रता से इसे आपूर्ति की गई ऊर्जा को अवशोषित करता है।

लेकिन क्या होगा यदि आप समय-समय पर दूसरे कारक (वर्तमान या वोल्टेज नहीं) को बदलते हैं, लेकिन पहला कारक - अधिष्ठापन या समाई? इस स्थिति में, परिपथ की ऊर्जा में भी परिवर्तन होगा।

उदाहरण के लिए, समय-समय पर कॉइल के अंदर और बाहर कोर को धकेलना या कैपेसिटर को अंदर और बाहर धकेलनाढांकता हुआ, - हमें परिपथ में ऊर्जा में एक बहुत ही निश्चित आवधिक परिवर्तन भी मिलता है।

हम इस स्थिति को कुंडल अधिष्ठापन में एक इकाई परिवर्तन के लिए लिखते हैं:

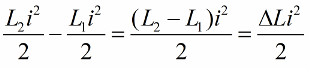
सर्किट के स्विंग का सबसे स्पष्ट प्रभाव तब होगा जब इंडक्शन परिवर्तन ठीक समय पर किए जाते हैं। उदाहरण के लिए, यदि हम किसी भी समय उसी सर्किट को लेते हैं, जब कुछ धारा i पहले से ही उसमें प्रवाहित हो रही है, और कॉइल में एक कोर पेश करते हैं, तो ऊर्जा निम्न राशि से बदल जाएगी:

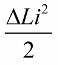
अब मुक्त दोलनों को सर्किट में ही प्रकट होने दें, लेकिन उस समय जब, एक चौथाई अवधि के बाद, ऊर्जा पूरी तरह से संधारित्र में पारित हो गई है और कॉइल में करंट शून्य हो गया है, हम कॉइल से कोर को अचानक हटा देंगे अधिष्ठापन प्रारंभिक मान L पर अपनी मूल स्थिति में वापस आ जाएगा। कोर को हटाए जाने पर चुंबकीय क्षेत्र के विरुद्ध कोई कार्य खर्च करने की आवश्यकता नहीं है। इसलिए, जब कोर को कॉइल में धकेला गया, तो सर्किट को ऊर्जा मिली, जब से हमने काम किया, जिसका मूल्य:

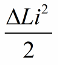
एक चौथाई अवधि के बाद, संधारित्र निर्वहन करना शुरू कर देता है, इसकी ऊर्जा फिर से कुंडल के चुंबकीय क्षेत्र की ऊर्जा में परिवर्तित हो जाती है।जब चुंबकीय क्षेत्र आयाम तक पहुंच जाता है, तो हम कोर को फिर से तेजी से दबाएंगे। फिर से अधिष्ठापन बढ़ा, उसी मात्रा में वृद्धि हुई।

और फिर से, शून्य करंट पर, हम इंडक्शन को उसके मूल मान पर लौटाते हैं। नतीजतन, यदि प्रत्येक आधे चक्र के लिए ऊर्जा का लाभ प्रतिरोध के नुकसान से अधिक हो जाता है, तो लूप की ऊर्जा हर समय बढ़ेगी और दोलन आयाम में वृद्धि होगी। यह स्थिति असमानता द्वारा व्यक्त की गई है:

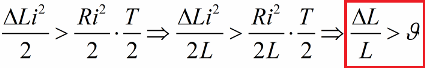
यहां हमने इस असमानता के दोनों पक्षों को एल से विभाजित किया और लॉगरिदमिक गिरावट के एक निश्चित मूल्य के लिए छलांग द्वारा पैरामीट्रिक उत्तेजना की संभावना के लिए शर्त लिखी।

प्रति अवधि दो बार अधिष्ठापन (या समाई) को बदलने की सिफारिश की जाती है, इसलिए पैरामीटर परिवर्तन की आवृत्ति (पैरामीट्रिक अनुनाद आवृत्ति) दोलन प्रणाली की प्राकृतिक आवृत्ति से दोगुनी होनी चाहिए:

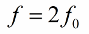
तो ईएमएफ या करंट को सीधे बदलने की आवश्यकता के बिना सर्किट में दोलनों के उत्तेजना का मार्ग दिखाई दिया है।सर्किट में शुरुआती उतार-चढ़ाव वाला करंट हमेशा एक या दूसरे तरीके से मौजूद होता है, और वह वातावरण में रेडियो फ्रीक्वेंसी दोलनों के हस्तक्षेप को भी ध्यान में नहीं रखता है।

यदि अधिष्ठापन (या समाई) छलांग में नहीं बदलता है, लेकिन सामंजस्यपूर्ण रूप से, तो दोलनों की घटना के लिए स्थिति थोड़ी अलग दिखाई देगी:

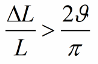
चूँकि कैपेसिटेंस और इंडक्शन सर्किट पैरामीटर हैं (जैसे कि पेंडुलम का द्रव्यमान या स्प्रिंग की लोच), रोमांचक दोलनों की विधि को पैरामीट्रिक उत्तेजना भी कहा जाता है।

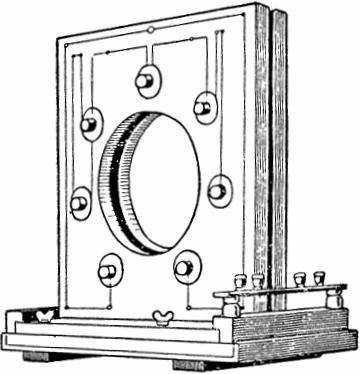
इस घटना की खोज और व्यावहारिक रूप से 20 वीं शताब्दी की शुरुआत में सोवियत भौतिकविदों मंडेलस्टम और पापालेक्सी द्वारा की गई थी। इस भौतिक घटना के आधार पर, उन्होंने 4 kW की शक्ति और चर अधिष्ठापन के साथ पहला पैरामीट्रिक एसी जनरेटर बनाया।

जनरेटर के डिजाइन में, फ्रेम के दोनों किनारों पर फ्लैट कॉइल के सात जोड़े स्थित थे, जिसके गुहा में प्रोट्रूशियंस के साथ एक फेरोमैग्नेटिक डिस्क घूमती थी। जब डिस्क को एक मोटर द्वारा घुमाने के लिए प्रेरित किया जाता है, तो इसके उभार समय-समय पर कॉइल के प्रत्येक जोड़े के बीच अंतरिक्ष में अंदर और बाहर चले जाते हैं, जिससे अधिष्ठापन और रोमांचक दोलन बदल जाते हैं।