प्रत्यावर्ती धारा परिपथ में शक्ति कारक के अप्रत्यक्ष निर्धारण का सिद्धांत और तरीके

पावर फैक्टर या कोसाइन फाई, साइनसॉइडल अल्टरनेटिंग करंट के उपयोगकर्ता के संबंध में, नेटवर्क से इस उपयोगकर्ता को आपूर्ति की जाने वाली कुल बिजली S की सक्रिय बिजली खपत P का अनुपात है।

कुल शक्ति एस, सामान्य स्थिति में, माना सर्किट में वर्तमान I और वोल्टेज U के प्रभावी (मूल माध्य वर्ग) मूल्यों के उत्पाद के रूप में परिभाषित किया जा सकता है, और सक्रिय शक्ति P - उपयोगकर्ता द्वारा अपरिवर्तनीय रूप से खपत के रूप में कार्य का संचालन।

प्रतिक्रियाशील शक्ति क्यू, हालाँकि यह कुल शक्ति का हिस्सा है, हालाँकि, इसका उपयोग कार्य करने के लिए नहीं किया जाता है, बल्कि उपयोगकर्ता के सर्किट के कुछ तत्वों में वैकल्पिक विद्युत और चुंबकीय क्षेत्रों के निर्माण में भाग लेता है।

के अलावा प्रत्यक्ष शक्ति कारक माप इलेक्ट्रोडायनामिक उपकरणों का उपयोग- चरण मीटर, काफी तार्किक अप्रत्यक्ष तरीके हैं जो आपको गणितीय रूप से इस महत्वपूर्ण विद्युत मात्रा के मूल्य को सटीक रूप से समझने की अनुमति देते हैं जो एक साइनसॉइडल वैकल्पिक चालू सर्किट में उपयोगकर्ता की विशेषता है।

आइए आंकड़ों पर नजर डालते हैं अप्रत्यक्ष तरीके विस्तार में, आइए अप्रत्यक्ष शक्ति कारक मापन के सिद्धांत को समझें।

वोल्टमीटर, एमीटर और वाटमीटर विधि

इलेक्ट्रोडायनामिक वाटमीटर इसके मूविंग कॉइल के सर्किट में अतिरिक्त सक्रिय प्रतिरोध के साथ एसी सर्किट पी में खपत होने वाली अत्यधिक सक्रिय शक्ति का मूल्य इंगित करता है।

यदि अब, एक वाल्टमीटर और एक एमीटर का उपयोग करते हुए, हम अध्ययन के तहत लोड के सर्किट में वर्तमान I और वोल्टेज U के औसत मान को मापते हैं, तो इन दो मापदंडों को गुणा करके, हमें केवल कुल शक्ति S मिलेगी .

फिर किसी दिए गए लोड का पावर फैक्टर (कोसाइन फाई) सूत्र का उपयोग करके आसानी से पाया जा सकता है:

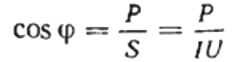
यहाँ, यदि आप चाहें, तो आप प्रतिक्रियाशील शक्ति Q का मान, सर्किट z का कुल प्रतिरोध भी पा सकते हैं ओम कानून, साथ ही सक्रिय और प्रतिक्रियाशील प्रतिरोध, बस एक प्रतिरोध त्रिकोण का निर्माण या प्रतिनिधित्व करके, और फिर पाइथागोरस प्रमेय का उपयोग करके:

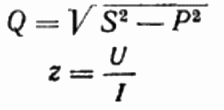
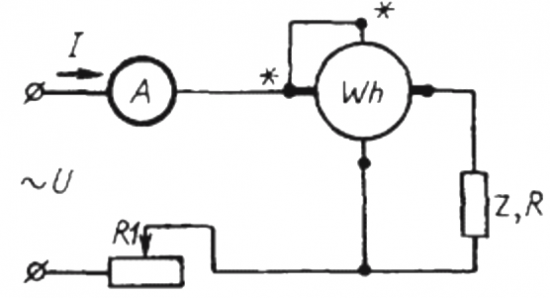
काउंटर और एमीटर विधि

इस पद्धति का उपयोग करने के लिए, एक सर्किट को इकट्ठा करना आवश्यक है जिसमें लोड जेड और एमीटर के साथ श्रृंखला में सरलतम जुड़ा हुआ है बिजली का मीटर क.

समय की एक निश्चित अवधि के लिए, एक मिनट के क्रम में, डिस्क एन के क्रांतियों की संख्या की गणना करना आवश्यक होगा, जो एक निश्चित समय के दौरान खर्च की गई सक्रिय ऊर्जा की मात्रा दिखाएगा (अर्थात, ध्यान में रखते हुए) ऊर्जा घटक)।

यहाँ: डिस्क N के क्रांतियों की संख्या, गुणांक k प्रति क्रांति ऊर्जा की मात्रा है, I और U क्रमशः rms करंट और वोल्टेज हैं, t क्रांतियों की गिनती का समय है, कोसाइन phi शक्ति कारक है:

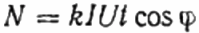
फिर, अध्ययन किए गए उपयोगकर्ता Z के बजाय, सक्रिय लोड R को उसी काउंटर के माध्यम से सर्किट में शामिल किया जाता है, लेकिन सीधे नहीं, बल्कि रिओस्टेट R1 के माध्यम से (उपयोगकर्ता Z के साथ पहले मामले में समान वर्तमान I प्राप्त करना)। डिस्क एन 1 के क्रांतियों की संख्या उसी समय टी के लिए बनाए रखी जाती है। लेकिन यहाँ, चूंकि लोड सक्रिय है, कोसाइन फाई (पावर फैक्टर) निश्चित रूप से 1 के बराबर है। इसलिए:

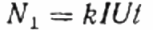
फिर डिस्क काउंटर के क्रांतियों का अनुपात पहले और दूसरे मामलों में समान अवधि के लिए दर्ज किया जाता है। यह कोसाइन फी होगा, यानी पहले लोड का पावर फैक्टर (उसी के साथ विशुद्ध रूप से सक्रिय लोड के सापेक्ष) मौजूदा):

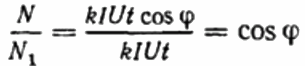
तीन एमीटर विधि

साइनसोइडल करंट सर्किट में तीन एमीटर का उपयोग करके पावर फैक्टर निर्धारित करने के लिए, आपको पहले निम्नलिखित सर्किट को इकट्ठा करना होगा:

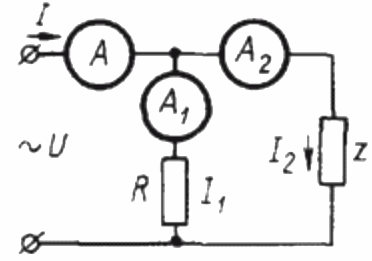
यहाँ Z एक भार है जिसका शक्ति गुणक निर्धारित किया जाना है और R विशुद्ध रूप से सक्रिय भार है।

चूंकि लोड आर विशुद्ध रूप से सक्रिय है, किसी भी समय वर्तमान I1 इस लोड पर लागू वैकल्पिक वोल्टेज यू के चरण में है। इस मामले में, वर्तमान I धाराओं I1 और I2 के ज्यामितीय योग के बराबर है। अब हम इस स्थिति के आधार पर धाराओं का एक वेक्टर आरेख बनाएंगे:

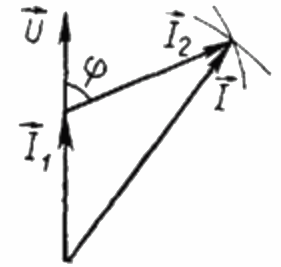
धाराओं के वेक्टर आरेख पर, वर्तमान I1 और वर्तमान I2 के बीच का तीव्र कोण कोण phi है, जिसका कोसाइन (वास्तव में, शक्ति कारक का मान) मूल्यों की एक विशेष तालिका से पाया जा सकता है त्रिकोणमितीय कार्यों या सूत्र द्वारा गणना की:

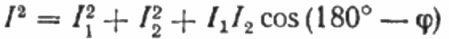
यहाँ से हम कोसाइन फाई व्यक्त कर सकते हैं, जो कि वांछित शक्ति कारक है:

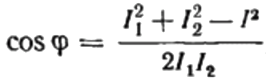
पाए गए पावर फैक्टर का चिह्न («+» या «-«) लोड की प्रकृति को इंगित करेगा। यदि शक्ति कारक (कोसाइन फाई) ऋणात्मक है, तो लोड प्रकृति में कैपेसिटिव है। यदि शक्ति गुणक धनात्मक मान है, तो भार की प्रकृति आगमनात्मक होती है।