भूतल प्रभाव और निकटता प्रभाव

प्रत्यक्ष धारा के लिए कंडक्टर का प्रतिरोध सुप्रसिद्ध सूत्र ro =ρl / S द्वारा निर्धारित किया जाता है।

यह प्रतिरोध निरंतर वर्तमान IO और पावर PO के परिमाण को जानकर भी निर्धारित किया जा सकता है:

आरओ = पीओ/एज़ो2

यह पता चला है कि एक प्रत्यावर्ती धारा परिपथ में, एक ही कंडक्टर का प्रतिरोध r प्रतिरोध स्थिरांक से अधिक होता है: r> rО

यह प्रतिरोध r प्रत्यक्ष धारा प्रतिरोध rO के विपरीत होता है और इसे सक्रिय प्रतिरोध कहा जाता है। तार प्रतिरोध में वृद्धि को इस तथ्य से समझाया गया है कि प्रत्यावर्ती धारा के साथ, तार के क्रॉस सेक्शन में विभिन्न बिंदुओं पर वर्तमान घनत्व समान नहीं होता है। मेरे पास कंडक्टर सतहें हैं, वर्तमान घनत्व प्रत्यक्ष प्रवाह से अधिक है, और केंद्र छोटा है।

उच्च आवृत्ति पर, अनियमितता इतनी तेजी से प्रकट होती है कि कंडक्टर के क्रॉस सेक्शन की एक महत्वपूर्ण केंद्रीय शुद्धता में वर्तमान घनत्व व्यावहारिक रूप से शून्य है। वर्तमान केवल सतह परत में गुजरता है, यही कारण है कि इस घटना को सतह प्रभाव कहा जाता है।

इस प्रकार, सतह प्रभाव कंडक्टर के क्रॉस-सेक्शन में कमी की ओर जाता है जिसके माध्यम से वर्तमान प्रवाह (सक्रिय क्रॉस-सेक्शन) होता है, और इसलिए प्रत्यक्ष वर्तमान प्रतिरोध की तुलना में इसके प्रतिरोध में वृद्धि होती है।

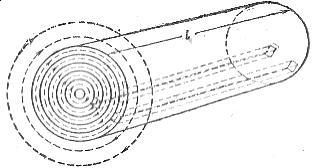
सतह के प्रभाव के कारण की व्याख्या करने के लिए, एक बेलनाकार कंडक्टर (छवि 1) की कल्पना करें, जिसमें एक ही क्रॉस-सेक्शन के बड़ी संख्या में प्राथमिक कंडक्टर शामिल हैं, जो एक दूसरे के करीब हैं और संकेंद्रित परतों में व्यवस्थित हैं।

सूत्र ρl / S द्वारा ज्ञात प्रत्यक्ष धारा के लिए इन तारों का प्रतिरोध समान होगा।

चावल। 1. बेलनाकार चालक का चुंबकीय क्षेत्र।

एक प्रत्यावर्ती विद्युत धारा प्रत्येक तार के चारों ओर एक वैकल्पिक चुंबकीय क्षेत्र बनाती है (चित्र 1)। जाहिर है, धुरी के करीब स्थित प्राथमिक कंडक्टर एक बड़े चुंबकीय प्रवाह सतह कंडक्टर से घिरा हुआ है, इसलिए पूर्व में उत्तरार्द्ध की तुलना में उच्च अधिष्ठापन और प्रेरक प्रतिक्रिया होती है।

अक्ष के साथ और सतह पर स्थित एल लंबाई के प्राथमिक तारों के सिरों पर एक ही वोल्टेज पर, पहले में वर्तमान घनत्व दूसरे की तुलना में कम है।

अंतर v अक्ष के साथ वर्तमान घनत्व और कंडक्टर की परिधि के साथ कंडक्टर डी के व्यास में वृद्धि के साथ बढ़ता है, सामग्री की चालकता γ, सामग्री μ और एसी आवृत्ति की चुंबकीय पारगम्यता।

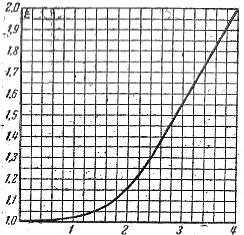
एक कंडक्टर आर के सक्रिय प्रतिरोध का अनुपात इसके प्रतिरोध पर। प्रत्यक्ष वर्तमान rО को त्वचा प्रभाव का गुणांक कहा जाता है और इसे ξ (xi) अक्षर से दर्शाया जाता है, इसलिए, गुणांक ξ को अंजीर में ग्राफ से निर्धारित किया जा सकता है। 2, जो उत्पाद d और √γμμое पर ξ की निर्भरता दर्शाता है।

चावल। 2. त्वचा प्रभाव गुणांक निर्धारित करने के लिए चार्ट।

इस उत्पाद की गणना करते समय, d को सेमी, γ - 1 / ओम-सेमी, μo - v gn/ सेमी और f = Hz में व्यक्त किया जाना चाहिए।

एक उदाहरण। त्वचा के प्रभाव के गुणांक को निर्धारित करना आवश्यक है क्योंकि मैं एफ = 150 हर्ट्ज की आवृत्ति पर डी = 11.3 मिमी (एस = 100 मिमी 2) के व्यास के साथ तांबा कंडक्टर हूं।

अच्छी नौकरी।

अंजीर में ग्राफ के अनुसार। 2 हम ξ = 1.03 पाते हैं

किसी चालक में असमान धारा घनत्व पड़ोसी चालकों में धाराओं के प्रभाव के कारण भी होता है। इस घटना को निकटता प्रभाव कहा जाता है।

दो समानांतर कंडक्टरों में एक ही दिशा में धाराओं के चुंबकीय क्षेत्र को ध्यान में रखते हुए, यह दिखाना आसान है कि अलग-अलग कंडक्टरों से संबंधित प्राथमिक कंडक्टर, जो एक दूसरे से सबसे दूर हैं, सबसे छोटे चुंबकीय प्रवाह से जुड़े हैं, इसलिए उनमें वर्तमान घनत्व सर्वोच्च है। यदि समानांतर तारों में धाराओं की अलग-अलग दिशाएँ हैं, तो यह दिखाया जा सकता है कि उन प्राथमिक तारों में एक उच्च वर्तमान घनत्व देखा जाता है जो अलग-अलग तारों से संबंधित होते हैं जो एक दूसरे के सबसे करीब होते हैं।