इंडक्शन की गणना कैसे करें

जिस तरह यांत्रिकी में द्रव्यमान वाला एक पिंड अंतरिक्ष में त्वरण का विरोध करता है, जड़ता प्रकट करता है, उसी प्रकार अधिष्ठापन एक चालक में धारा को बदलने से रोकता है, स्व-प्रेरण EMF को प्रकट करता है। यह स्व-प्रेरण का EMF है, जो वर्तमान में कमी, इसे बनाए रखने की कोशिश और वर्तमान में वृद्धि, इसे कम करने की कोशिश दोनों का विरोध करता है।

तथ्य यह है कि सर्किट में करंट को बदलने (बढ़ने या घटने) की प्रक्रिया में, इस करंट द्वारा बनाया गया चुंबकीय प्रवाह भी बदल जाता है, जो मुख्य रूप से इस सर्किट द्वारा सीमित क्षेत्र में स्थानीयकृत होता है। और जैसे ही चुंबकीय प्रवाह बढ़ता या घटता है, यह स्व-प्रेरण का ईएमएफ प्रेरित करता है (लेनज़ के नियम के अनुसार - उस कारण के खिलाफ जो इसका कारण बनता है, यानी शुरुआत में उल्लिखित वर्तमान के खिलाफ), सभी एक ही सर्किट में। यहाँ अधिष्ठापन L को वर्तमान I और कुल चुंबकीय प्रवाह Φ के बीच आनुपातिकता कारक कहा जाता है, यह वर्तमान द्वारा उत्पन्न होता है:

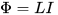
तो, सर्किट का अधिष्ठापन जितना अधिक होता है, परिणामी चुंबकीय क्षेत्र की तुलना में यह उतना ही मजबूत होता है, यह करंट को बदलने से रोकता है (यह वह क्षेत्र है जो इसे बनाता है) और इसलिए वर्तमान को अधिक अधिष्ठापन के माध्यम से बदलने में अधिक समय लगेगा, समान लागू वोल्टेज के साथ। निम्नलिखित कथन भी सत्य है: अधिष्ठापन जितना अधिक होगा, सर्किट में वोल्टेज उतना ही अधिक होगा जब इसके माध्यम से चुंबकीय प्रवाह बदल जाएगा।

मान लीजिए कि हम एक निश्चित क्षेत्र में एक स्थिर दर पर चुंबकीय प्रवाह को बदलते हैं, तो इस क्षेत्र को विभिन्न सर्किटों के साथ कवर करके, हम उस सर्किट पर अधिक वोल्टेज प्राप्त करेंगे जिसका अधिष्ठापन अधिक है (ट्रांसफार्मर, रमकोर्फ कॉइल, आदि इस सिद्धांत पर काम करता है)।

लेकिन लूप इंडक्शन की गणना कैसे की जाती है? वर्तमान और चुंबकीय प्रवाह के बीच आनुपातिकता कारक कैसे ज्ञात करें? याद रखने वाली पहली बात यह है कि हेनरी (एच) में अधिष्ठापन बदल जाता है। 1 हेनरी के अधिष्ठापन वाले सर्किट के टर्मिनलों पर, यदि इसमें करंट प्रति सेकंड एक एम्पीयर बदलता है, तो 1 वोल्ट का वोल्टेज दिखाई देगा।

अधिष्ठापन का परिमाण दो मापदंडों पर निर्भर करता है: सर्किट के ज्यामितीय आयामों पर (लंबाई, चौड़ाई, घुमावों की संख्या, आदि) और माध्यम के चुंबकीय गुणों पर (यदि, उदाहरण के लिए, अंदर एक फेराइट कोर है) कॉइल, इसका इंडक्शन अधिक होगा, अगर अंदर कोई कोर नहीं है)।

उत्पादित अधिष्ठापन की गणना करने के लिए, यह जानना आवश्यक है कि कुंडल स्वयं किस आकार का होगा और इसके अंदर के माध्यम में चुंबकीय पारगम्यता क्या होगी (माध्यम की सापेक्ष चुंबकीय पारगम्यता एक निर्वात की चुंबकीय पारगम्यता और चुंबकीय पारगम्यता के बीच आनुपातिकता कारक है किसी दिए गए माध्यम की पारगम्यता।बेशक, यह विभिन्न सामग्रियों के लिए अलग है) ...

आइए कॉइल के सबसे सामान्य रूपों (बेलनाकार सोलनॉइड, टॉरॉयड और लंबे तार) के अधिष्ठापन की गणना के लिए सूत्र देखें।

यहाँ अधिष्ठापन की गणना करने का सूत्र है solenoid — कुंडल, जिसकी लंबाई व्यास से बहुत अधिक है:

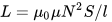
जैसा कि आप देख सकते हैं, N घुमावों की संख्या, घुमावदार l की लंबाई और कॉइल S के क्रॉस-सेक्शनल क्षेत्र को जानने के बाद, हम कोर के बिना या कोर के साथ कॉइल का अनुमानित अधिष्ठापन पाते हैं, जबकि चुंबकीय निर्वात की पारगम्यता एक स्थिर मान है:

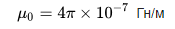
टॉरॉयडल कॉइल का इंडक्शन, जहां h टॉरॉयड की ऊंचाई है, r टॉरॉयड का आंतरिक व्यास है, R टॉरॉयड का बाहरी व्यास है:

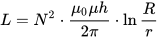
एक पतले तार का अधिष्ठापन (क्रॉस-सेक्शन का त्रिज्या लंबाई से बहुत छोटा है), जहां l तार की लंबाई है, और r इसके क्रॉस-सेक्शन की त्रिज्या है। Mu सूचकांकों i और e के साथ हैं आंतरिक (आंतरिक, कंडक्टर सामग्री) और बाहरी (बाहरी, कंडक्टर के बाहर की सामग्री) वातावरण की सापेक्ष चुंबकीय पारगम्यता:

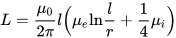
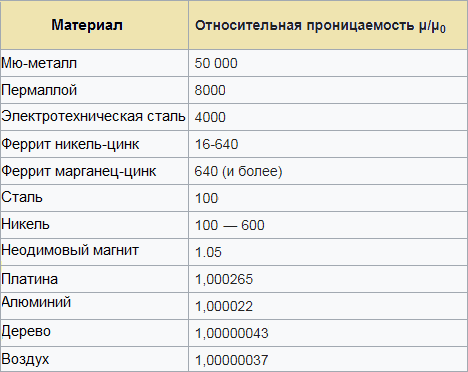
सापेक्ष परमिट की एक तालिका आपको यह अनुमान लगाने में मदद करेगी कि एक कोर के रूप में एक निश्चित चुंबकीय सामग्री का उपयोग करके आप एक सर्किट (तार, कुंडल) से किस अधिष्ठापन की उम्मीद कर सकते हैं: