वर्तमान और वोल्टेज के आरएमएस मूल्य

प्रत्यावर्ती साइनसोइडल करंट की अवधि के दौरान अलग-अलग तात्कालिक मूल्य होते हैं। यह प्रश्न उठना स्वाभाविक है कि परिपथ में सम्मिलित अमीटर से धारा का कौन-सा मान मापा जायेगा?

वैकल्पिक चालू सर्किट, साथ ही विद्युत माप की गणना करते समय, धाराओं और वोल्टेज के तात्कालिक या आयाम मूल्यों का उपयोग करना असुविधाजनक होता है, और एक अवधि में उनके औसत मूल्य शून्य होते हैं। इसके अलावा, समय-समय पर बदलते करंट (जारी की गई गर्मी की मात्रा, सही संचालन, आदि) के विद्युत प्रभाव का अनुमान इस करंट के आयाम से नहीं लगाया जा सकता है।

सबसे सुविधाजनक वर्तमान और वोल्टेज के तथाकथित प्रभावी मूल्यों की अवधारणाओं का परिचय था। ये अवधारणाएं वर्तमान की तापीय (या यांत्रिक) क्रिया पर आधारित हैं, जो इसकी दिशा पर निर्भर नहीं करती है।

प्रत्यावर्ती धारा का मूल माध्य वर्ग मान - यह प्रत्यक्ष धारा का वह मान है जिस पर प्रत्यावर्ती धारा की अवधि के दौरान कंडक्टर में उतनी ही मात्रा में ऊष्मा जारी की जाती है जितनी कि प्रत्यावर्ती धारा के दौरान।

की गई कार्रवाइयों का मूल्यांकन करने के लिए प्रत्यावर्ती धारा, हम इसकी क्रियाओं की तुलना दिष्टधारा के ऊष्मीय प्रभाव से करेंगे।

प्रतिरोध r से गुजरने वाली DC पावर P A, P = P2r होगी।

AC पावर को पूरी अवधि में तात्क्षणिक पावर Az2r के औसत प्रभाव या उसी समय के लिए (I am x sinωT)2 NS r के औसत के रूप में व्यक्त किया जाता है।

मान लें कि अवधि के लिए t2 का औसत मान M है। प्रत्यक्ष धारा की शक्ति और प्रत्यावर्ती धारा की शक्ति के बराबर होने पर, हमारे पास: Az2r = Mr -n, जहां से Az = √M,

मात्रा I को प्रत्यावर्ती धारा का प्रभावी मान कहा जाता है।

प्रत्यावर्ती धारा में i2 का औसत मान निम्नानुसार निर्धारित किया जाता है।

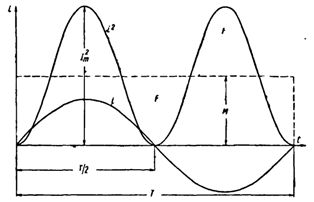
आइए एक ज्यावक्रीय धारा वक्र का निर्माण करें। प्रत्येक तात्कालिक वर्तमान मूल्य का वर्ग करके, हम एक P बनाम समय वक्र प्राप्त करते हैं।

एसी आरएमएस मूल्य

इस वक्र के दोनों आधे भाग क्षैतिज अक्ष के ऊपर स्थित हैं, क्योंकि अवधि के दूसरे भाग में ऋणात्मक धाराएँ (-i) जब चुकता की जाती हैं, तो सकारात्मक मान देती हैं।

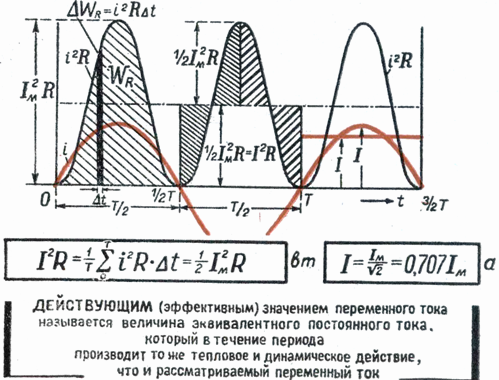
आधार टी और वक्र i2 और क्षैतिज अक्ष से घिरे क्षेत्र के बराबर क्षेत्रफल के साथ एक आयत की रचना करें। आयत M की ऊँचाई अवधि के लिए P के औसत मान के अनुरूप होगी। उच्च गणित का उपयोग करके गणना की गई अवधि का यह मान 1/2 I2m के बराबर होगा... इसलिए, M. = 1/2 I2m

चूँकि rms मान Im प्रत्यावर्ती धारा है Im = √Mतो अंत में I = Im / √2

इसी तरह, वोल्टेज यू और ई के लिए आरएमएस और आयाम मूल्यों के बीच संबंध का रूप है:

यू = उम / √2E = ईएम / √2

चर के प्रभावी मूल्यों को सबस्क्रिप्ट (I, U, E) के बिना बड़े अक्षरों में दर्शाया गया है।

उपरोक्त के आधार पर, हम कह सकते हैं कि एक प्रत्यावर्ती धारा का प्रभावी मान उस प्रत्यक्ष धारा के बराबर होता है, जो प्रत्यावर्ती धारा के समान प्रतिरोध से गुजरते हुए, एक ही समय में उतनी ही मात्रा में ऊर्जा मुक्त करती है।

एक वैकल्पिक चालू सर्किट में शामिल विद्युत माप उपकरण (एमीटर, वोल्टमीटर) वर्तमान या वोल्टेज के प्रभावी मूल्यों को इंगित करते हैं।

वेक्टर आरेखों का निर्माण करते समय, आयाम को नहीं, बल्कि वैक्टर के प्रभावी मूल्यों को स्थगित करना अधिक सुविधाजनक होता है। इसके लिए, सदिशों की लंबाई को एक बार √2 कम कर दिया जाता है। यह आरेख पर वैक्टरों का स्थान नहीं बदलता है।