आवेग वर्तमान

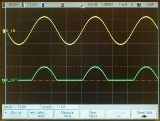विभिन्न इलेक्ट्रॉनिक उपकरणों में, उदाहरण के लिए, इलेक्ट्रॉनिक और सेमीकंडक्टर उपकरण में, यानी एम्पलीफायरों, रेक्टीफायर्स, रेडियो, जेनरेटर, टीवी, साथ ही साथ कार्बन माइक्रोफोन, टेलीग्राफ और कई अन्य उपकरणों में, वे व्यापक रूप से तरंग धाराओं और वोल्टेज का उपयोग करते हैं ... क्रम में तर्क को दो बार न दोहराने के लिए, हम केवल धाराओं के बारे में बात करेंगे, लेकिन धाराओं से संबंधित हर चीज वोल्टेज के लिए भी सही है।

स्पंदित धाराएँ जिनकी एक स्थिर दिशा होती है लेकिन उनका मान भिन्न हो सकता है। कभी-कभी वर्तमान मान उच्चतम से निम्नतम गैर-शून्य मान में बदल जाता है। अन्य मामलों में, वर्तमान को घटाकर शून्य कर दिया जाता है। अगर प्रत्यक्ष वर्तमान सर्किट एक निश्चित आवृत्ति पर बाधित होता है, तो कुछ समय के अंतराल के लिए सर्किट में कोई करंट नहीं होता है।

अंजीर में। 1 विभिन्न तरंग धाराओं के रेखांकन दिखाता है। अंजीर में। 1, ए, बी, धाराओं में परिवर्तन के अनुसार होता है साइनसोइडल वक्र, लेकिन इन धाराओं को साइनसॉइडल वैकल्पिक धाराओं के रूप में नहीं माना जाना चाहिए, क्योंकि वर्तमान की दिशा (संकेत) नहीं बदलती है। अंजीर में।1, c अलग-अलग दालों से मिलकर एक धारा दिखाता है, जो कि वर्तमान के अल्पकालिक "झटके" हैं, जो अधिक या कम अवधि के ठहराव द्वारा एक दूसरे से अलग होते हैं, और अक्सर इसे स्पंदित धारा कहा जाता है। अलग-अलग स्पंदित धाराएं स्पंदों के आकार और अवधि के साथ-साथ पुनरावृत्ति की दर में एक दूसरे से भिन्न होती हैं।

किसी भी प्रकार की स्पंदित धारा को दो धाराओं - प्रत्यक्ष और प्रत्यावर्ती धारा के योग के रूप में विचार करना सुविधाजनक है, जिसे शब्द या घटक धाराएँ कहा जाता है। किसी भी स्पंदनशील धारा में DC और AC घटक होते हैं। यह बहुतों को अजीब लगता है। वास्तव में, आखिरकार, एक स्पंदित धारा एक धारा है जो हर समय एक दिशा में बहती है और इसके मूल्य को बदलती है।

आप कैसे बता सकते हैं कि इसमें प्रत्यावर्ती धारा है जो दिशा बदलती है? हालाँकि, यदि दो धाराएँ - प्रत्यक्ष और प्रत्यावर्ती - एक ही तार से एक साथ गुजरती हैं, तो यह पता चलता है कि उस तार में एक स्पंदित धारा प्रवाहित होगी (चित्र 2)। इस मामले में, प्रत्यावर्ती धारा का आयाम प्रत्यक्ष धारा के मान से अधिक नहीं होना चाहिए। प्रत्यक्ष और प्रत्यावर्ती धाराएँ तार के माध्यम से अलग-अलग प्रवाहित नहीं हो सकती हैं। वे इलेक्ट्रॉनों के एक सामान्य प्रवाह में जोड़ते हैं जिसमें एक स्पंदित धारा के सभी गुण होते हैं।

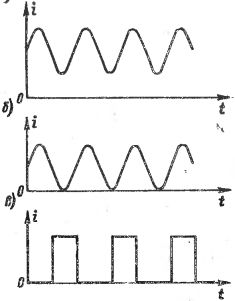
चावल। 1. विभिन्न तरंग धाराओं के रेखांकन

एसी और डीसी धाराओं के जोड़ को ग्राफिकल रूप से दिखाया जा सकता है। अंजीर में। 2 15 mA के बराबर दिष्ट धारा और 10 mA के आयाम वाली एक प्रत्यावर्ती धारा के आलेख दिखाता है। यदि हम समय में अलग-अलग बिंदुओं के लिए इन धाराओं के मूल्यों को जोड़ते हैं, तो धाराओं की दिशाओं (संकेतों) को ध्यान में रखते हुए, हमें अंजीर में दिखाया गया तरंग वर्तमान ग्राफ मिलता है। 2 एक बोल्ड लाइन के साथ। यह करंट 5 mA के निम्न से लेकर 25 mA के उच्च तक भिन्न होता है।

धाराओं का माना गया जोड़ प्रत्यक्ष और वैकल्पिक धाराओं के योग के रूप में स्पंदित धारा के प्रतिनिधित्व की वैधता की पुष्टि करता है। इस प्रतिनिधित्व की शुद्धता की पुष्टि इस तथ्य से भी होती है कि कुछ उपकरणों की मदद से इस करंट के घटकों को एक दूसरे से अलग करना संभव है।

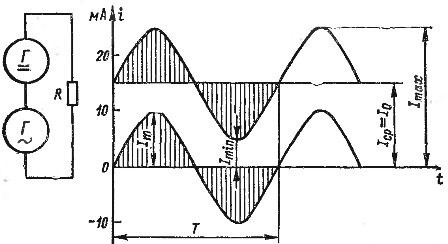
चावल। 2. प्रत्यक्ष और प्रत्यावर्ती धारा को जोड़कर एक स्पंदित धारा प्राप्त करना।

इस बात पर जोर दिया जाना चाहिए कि किसी भी धारा को हमेशा कई धाराओं के योग के रूप में दर्शाया जा सकता है। उदाहरण के लिए, 5 A की धारा को एक दिशा में बहने वाली धाराओं 2 और 3 A का योग माना जा सकता है, या अलग-अलग दिशाओं में बहने वाली धाराओं 8 और 3 A का योग, यानी दूसरे शब्दों में, धाराओं 8 के बीच का अंतर और 3 ए। कुल 5 ए देने वाले दो या दो से अधिक धाराओं के अन्य संयोजनों को खोजना मुश्किल नहीं है।

यहाँ बलों के योग और अपघटन के सिद्धांत के साथ पूर्ण समानता है। यदि दो समान रूप से निर्देशित बल किसी वस्तु पर कार्य करते हैं, तो उन्हें एक सामान्य बल द्वारा प्रतिस्थापित किया जा सकता है। विपरीत दिशाओं में कार्य करने वाले बलों को एक इकाई अंतर से बदला जा सकता है। इसके विपरीत, किसी दिए गए बल को हमेशा समान रूप से निर्देशित बलों का योग या विपरीत रूप से निर्देशित बलों के बीच का अंतर माना जा सकता है।

प्रत्यक्ष या साइनसोइडल वैकल्पिक धाराओं को घटक धाराओं में विघटित करना आवश्यक नहीं है। यदि हम स्पंदित धारा को प्रत्यक्ष और प्रत्यावर्ती धाराओं के योग से प्रतिस्थापित करते हैं, तो प्रत्यक्ष और प्रत्यावर्ती धाराओं के ज्ञात नियमों को इन घटक धाराओं पर लागू करके, कई समस्याओं को हल करना और स्पंदित धारा से संबंधित आवश्यक गणना करना संभव है।

प्रत्यक्ष और प्रत्यावर्ती धाराओं के योग के रूप में स्पंदित धारा की अवधारणा पारंपरिक है।बेशक, यह नहीं माना जा सकता है कि निश्चित समय अंतराल पर प्रत्यक्ष और प्रत्यावर्ती धाराएं वास्तव में तार के साथ एक दूसरे की ओर बहती हैं। वास्तव में, इलेक्ट्रॉनों के दो विपरीत प्रवाह नहीं होते हैं।

वास्तव में, एक स्पंदित धारा एक एकल धारा है जो समय के साथ अपना मान बदलती है। यह कहना अधिक सही है कि स्पंदित वोल्टेज या स्पंदित ईएमएफ को स्थिर और चर घटकों के योग के रूप में दर्शाया जा सकता है।

उदाहरण के लिए, चित्र में। 2 दिखाता है कि कैसे बीजगणितीय रूप से एक जनरेटर के स्थिर ईएमएफ को दूसरे जनरेटर के चर ईएमएफ में जोड़ा जाता है। नतीजतन, हमारे पास एक स्पंदित ईएमएफ है जो संबंधित स्पंदनशील धारा का कारण बनता है। सशर्त रूप से, हालांकि, यह माना जा सकता है कि एक निरंतर EMF सर्किट में एक प्रत्यक्ष धारा बनाता है, और एक वैकल्पिक EMF - एक प्रत्यावर्ती धारा, जिसे अभिव्यक्त करने पर, एक स्पंदित धारा बनती है।

प्रत्येक स्पंदनशील धारा को इटैक्स और इटिन के अधिकतम और न्यूनतम मूल्यों के साथ-साथ इसके स्थिर और परिवर्तनशील घटकों द्वारा चित्रित किया जा सकता है। स्थिर घटक को I0 द्वारा निरूपित किया जाता है। यदि प्रत्यावर्ती घटक एक साइनसोइडल करंट है, तो इसके आयाम को इसके द्वारा निरूपित किया जाता है (इन सभी मात्राओं को चित्र 2 में दिखाया गया है)।

इसे इट और इटैक्स के साथ भ्रमित नहीं होना चाहिए। साथ ही, वर्तमान तरंग आईमैक्स के अधिकतम मूल्य को आयाम नहीं कहा जाना चाहिए। आयाम शब्द आमतौर पर केवल वैकल्पिक धाराओं को संदर्भित करता है। स्पंदित धारा के संबंध में, हम केवल इसके चर घटक के आयाम के बारे में बात कर सकते हैं।

स्पंदित धारा के निरंतर घटक को इसका औसत मान Iav कहा जा सकता है, अर्थात अंकगणितीय औसत मान। दरअसल, अगर हम अंजीर में दिखाए गए पल्सेटिंग करंट की एक अवधि में बदलाव पर विचार करें।2, निम्नलिखित स्पष्ट रूप से देखा गया है: पहले आधे चक्र में, वर्तमान घटक को बदलकर 15 mA करंट में कई मान जोड़े जाते हैं, 0 से 10 mA और वापस 0 से भिन्न होते हैं, और दूसरी छमाही में -चक्र, ठीक उसी वर्तमान मान को वर्तमान 15 mA से घटाया जाता है।

इसलिए, 15 mA की धारा वास्तव में औसत मान है। चूँकि करंट तार के क्रॉस-सेक्शन के माध्यम से विद्युत आवेशों का स्थानांतरण है, तो Iav ऐसे प्रत्यक्ष करंट का मान है जो एक अवधि में (या पूरी अवधि के लिए) उतनी ही मात्रा में बिजली का वहन करता है जितना कि यह स्पंदित धारा .

साइनसॉइडल अल्टरनेटिंग करंट के लिए, Iav प्रति अवधि का मान शून्य है क्योंकि एक आधे-अवधि में कंडक्टर के क्रॉस-सेक्शन से गुजरने वाली बिजली की मात्रा दूसरी छमाही के दौरान विपरीत दिशा में गुजरने वाली बिजली की मात्रा के बराबर होती है। वर्तमान i की समय t पर निर्भरता दिखाने वाले धाराओं के ग्राफ़ पर, वर्तमान द्वारा की जाने वाली बिजली की मात्रा को वर्तमान वक्र द्वारा बंधे हुए आंकड़े के क्षेत्र द्वारा व्यक्त किया जाता है, क्योंकि बिजली की मात्रा द्वारा निर्धारित की जाती है उत्पाद है कि यह।

एक ज्यावक्रीय धारा के लिए, धनात्मक और ऋणात्मक आधी तरंगों के क्षेत्र समान होते हैं। अंजीर में दिखाए गए स्पंदित धारा में। 2, पहली छमाही के दौरान एसी घटक द्वारा ले जाने वाली बिजली की मात्रा को वर्तमान Iav (चित्र में छायांकित क्षेत्र) द्वारा ले जाने वाली बिजली की मात्रा में जोड़ा जाता है। और दूसरे आधे चक्र के दौरान ठीक उतनी ही मात्रा में बिजली निकाली जाती है। नतीजतन, पूरी अवधि में बिजली की समान मात्रा को एकल प्रत्यक्ष वर्तमान Iav के साथ स्थानांतरित किया जाता है, अर्थात आयत Iav T का क्षेत्रफल तरंग वर्तमान वक्र से घिरे क्षेत्र के बराबर होता है।

इस प्रकार, निरंतर घटक या वर्तमान का औसत मूल्य तार के क्रॉस सेक्शन के माध्यम से विद्युत आवेशों के हस्तांतरण द्वारा निर्धारित किया जाता है।

अंजीर में दिखाया गया वर्तमान समीकरण। 2 स्पष्ट रूप से निम्नलिखित रूप में लिखा जाना चाहिए:

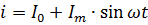
स्पंदित धारा की शक्ति की गणना उसके घटक धाराओं की शक्तियों के योग के रूप में की जानी चाहिए। उदाहरण के लिए, यदि वर्तमान चित्र में दिखाया गया है। 2, प्रतिरोध R के प्रतिरोध से होकर गुजरता है, तो इसकी शक्ति है

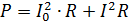
जहाँ I = 0.7Im चर घटक का rms मान है।

आप वेव करंट Id के rms मान की अवधारणा का परिचय दे सकते हैं। शक्ति की गणना सामान्य तरीके से की जाती है:

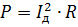
इस अभिव्यक्ति को पिछले एक के बराबर करना और इसे R से कम करना, हमें मिलता है:

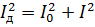
तनाव के लिए समान संबंध प्राप्त किए जा सकते हैं।